Noah tiene un dilema. El debe dividir una pizza en varias (posiblemente cero) piezas. Cada corte debe ser una línea recta entre el centro de la pizza a su frontera. Además, el ángulo entre los dos cortes debe tener un valor entero positivo (la medida de los ángulos en grados). Noah considerara dos pedazos de pizza iguales si sus ángulos correspondientes son iguales.

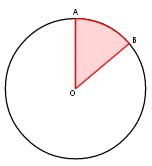
La imagen contiene dos piezas distintas, y dos cortes. La porción roja de la imagen muestra una pieza. El ángulo apropiado es AOB.

A Noah da se le proposrciona el valor N, que indica el número de piezas que debe cortar. Noah debe responder a las siguientes preguntas:

¿Es posible cortar exactamente N piezas iguales de toda la pizza?
¿Es posible cortar exactamente N piezas de toda el pizza?
¿Es posible cortar exactamente N piezas de toda la pizza, de tal manera que dos piezas no sean iguales?

Input

La primera línea del INPUT comienza con un número M que indica el número de casos del problema propuesto. (1 ≤ M ≤ 100)

Cada caso está compuesto de la(s) siguiente(s) linea(s):

La única contiene un solo número entero N , que denota el número de piezas que Noah quiere hacer. ( 1 ≤ C ≤ 10000 ).

Output

Para cada caso de prueba, la salida de una línea que contiene 3 caracteres separados por espacios.

Antes hemos definido las 3 preguntas que Noah preguntará. Imprimir 'S' para sí o "N" para no, para cada una de esas preguntas.

Imprimir las respuestas para 3 preguntas (en el orden de especificado), todas las respuestas deben estar separadas por un espacios en la misma línea.

Entrada de ejemplo

Explicación

Ejemplo caso 1.

¿Es posible hacer N piezas iguales? Sí, Noah puede cortar 4 pedazos cada uno con ángulo de 90 grados. ¿Es posible hacer N piezas? Sí, Noah puede cortar 4 pedazos cada uno con un ángulo de 90 grados. ¿Es posible hacer N piezas, de tal manera que no hay dos que sean iguales? Sí, Noah puede cortar 4 piezas con ángulos de 88, 89, 91, 92.