Plazas Libres
2 soluciones
1500 puntos
Un tren consiste en N bagones. Vamos a considerar un bagon en particular. Este cuenta con 54 plazas numeradas correlativamente del 1 al 54, algunas de las cuales ya están reservadas y algunas todavía están libres. Los lugares están numerados de la siguiente manera:
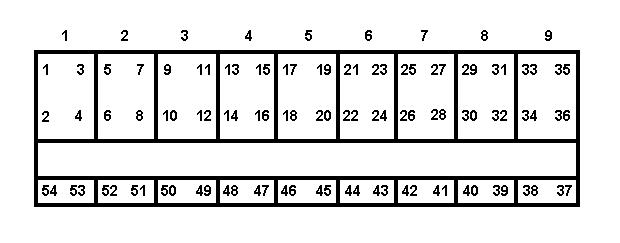
El bagon se separa en 9 compartimentos de 6 plazas cada uno, como se muestra en la imagen. Así, el primer compartimento consta de los siguientes lugares 1, 2, 3, 4, 53 y 54, el segundo compartimento consta de los lugares 5, 6, 7, 8, 51 y 52, y así sucesivamente.
Un grupo de X amigos quiere comprar entradas para los lugares libres, los cuales estén en un mismo compartimento (pues es mucho más divertido viajar juntos). Se le da la información sobre los lugares libres y reservados en cada uno de los N bagones. Encuentre el número de formas en que se puede vender X boletos al grupo de amigos en un mismo compartimiento (tenga en cuenta que el orden en el que se venden los boletos no importa).
Input
La primera línea del INPUT comienza con un número M que indica el número de casos del problema propuesto. (1 ≤ M ≤ 100)
Cada caso está compuesto de la(s) siguiente(s) linea(s):
La primera línea de cada caso contiene dos enteros X y N (1 ≤ X ≤ 6, 1 ≤ N ≤ 10), separados por un solo espacio. El número de amigos y el número de bagones del tren respectivamente.
Las siguientes N líneas contiene la información sobre un bagon que es una cadena de longitud 54 que consiste en '0 'y '1'. El i-ésimo carácter (numeradas de 1) es '0' si el lugar i correspondiente está libre, y es '1 'si el lugar i ya está reservado.
Output
Salida, un solo número entero - el número solicitado de maneras en que se puede vender X boletos.
Entrada de ejemplo
Input |
3 |
Output |
85 |
Explicación
En el primer caso de prueba, cualquiera de los lugares libres se pueden vender.
En el segundo caso de prueba, el único compartimento libre en el tren es el compartimiento 3 en el primer bagon donde ( 9, 10, 11, 12, 49 y 50 son las plazas libres).
En el tercer caso de prueba, el tren está absolutamente libre; ya que hay 20 maneras de vender 3 entradas en un compartimiento vacío, la respuesta es 2 * 9 * 20 = 360.