El Dr. Joel está a punto de enviar un mensaje a Sherlock Holmes. Él tiene una cadena de texto "S".

Una cadena de texto "P" se le llama una subcadena de la cadena S si se puede leer a partir de cierta posición en la cadena S. Por ejemplo, la cadena "aba" tiene seis subcadenas que serían: "a", "b", "a", "ab", "ba", "aba".

Dr. Joel planea tomar la cadena de texto S y cortar alguna subcadena de ella, a esta cadena vamos a llamarlo "T". Luego se tiene que cambiar la subcadena T cero o más veces. Y como resultado él debe obtener una nueva cadena "U" (Esta será la cadena de texto que debe ser enviada a Sherlock Holmes).

Un cambio en una cadena de texto se define como el resultado de una de las siguientes acciones:

- Insertar una letra a cualquier extremo de la cadena.
- Eliminar una letra desde cualquier extremo de la cadena.
- Cambiar una letra por cualquier otra.

Veamos el siguiente ejemplo:

El Dr. Joel es muy inteligente y después eligir una subcadena T, hace que el número mínimo de cambios en esta cadena para obtener la cadena U.

Ayude al Dr. Joel a elegir la mejor subcadena T de todas las subcadenas de la cadena S. La subcadena T debería minimizar el número de cambios que Joel debe hacer para obtener la cadena U.

Input

La primera línea del INPUT comienza con un número M que indica el número de casos del problema propuesto. (1 ≤ M ≤ 100)

Cada caso está compuesto de la(s) siguiente(s) linea(s):

- La primera línea contiene una cadena de texto S no vacía, que consiste en letras latinas en minúsculas.
- La segunda línea contiene una cadena de texto U no vacía, que consiste en letras latinas en minúsculas.
- Las longitudes de las dos cadenas están en el rango de 1 a 2000, inclusive.

Output

Imprimir un número, el número mínimo de cambios que el Dr. Joel tiene que hacer con la cadena que elija.

Entrada de ejemplo

Nota

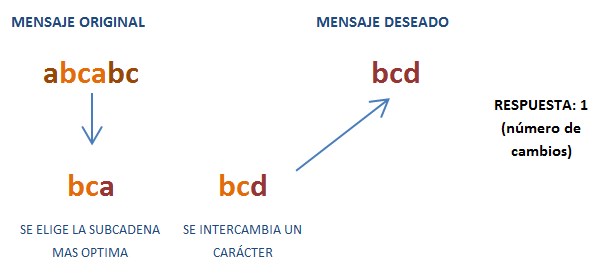
En el primer caso el Dr. Joel puede tomar cualquiera de las subcadenas de longitud 3, y que será igual al mensaje deseado de la cadena U, por lo que el Dr. no tendrá que realizar ningún cambio.

En el segundo caso debe tomar una subcadena formada por los caracteres del segundo al cuarto ("bca") o de la quinta a sexta parte ("ac"). A continuación, sólo tendrá que hacer un cambio: para cambiar o para añadir el último carácter.

En el tercer caso la cadena S inicial no contiene ningún carácter que el mensaje de la cadena U debe contener, por lo que, cualquiera que sea la subcadena que elija, tendrá que hacer por lo menos 7 cambios para obtener el mensaje deseado.