Un día Paolo encontró un diário que tenía N nombres escritos con una caracteristica inusual, cada nombre era exactamente de M caracteres. Enumerados de 1 a N en el orden en que se escriben.

Paolo decidió jugar con los nombres: él eligió tres números enteros positivos I, J, K, donde ( 1 ≤ I < J ≤ N, 1 ≤ K ≤ M), entonces él tomó nombres de los números I y J y cambió su prefijos de longitud K. Por ejemplo, si tomamos los nombres "CBDAD" y "AABRD", al cambiar sus prefijos con la longitud 3.

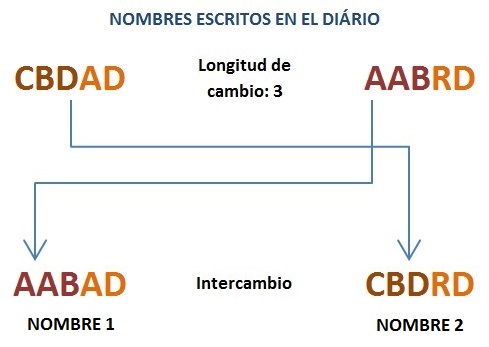
Paolo se pregunta cuantos nombres diferentes puede escribir en lugar del nombre número 1 del diário, se le permite a Paolo realizar cualquier número de las acciones descritas. Como Paolo realiza la misma acción varias veces, elige los números I, J, K, independientemente de los movimientos anteriores y su elección se basa totalmente en sus reglas.

Nota: El número buscado puede ser muy grande, por lo que sólo debe encontrar el número con modulo 1000000007 (10 ^ 9 + 7).

Input

La primera línea del INPUT comienza con un número M que indica el número de casos del problema propuesto. (1 ≤ M ≤ 100)

Cada caso está compuesto de la(s) siguiente(s) linea(s):

La primera línea de cada caso contiene dos enteros N y M (1 ≤ N, M ≤ 100), que son el número de nombres y la longitud de cada nombre, correspondientemente.

Seguido continuan N líneas que contienen nombres, cada nombre se compone de exactamente M mayúsculas de letras latinas.

Output

Imprimir un número, el número de nombres diferentes que se pueden encontrar del nombre en la posición número 1 del diário después de la aplicación de los procedimientos descritos anteriormente. Imprimir el número con módulo 1000000007 (10 ^ 9 + 7).

Entrada de ejemplo

Nota

En el primer caso Paolo puede obtener los siguientes nombres del nombre en el puesto número 1: "AAB", "AAA", "BAA" y "BAB".